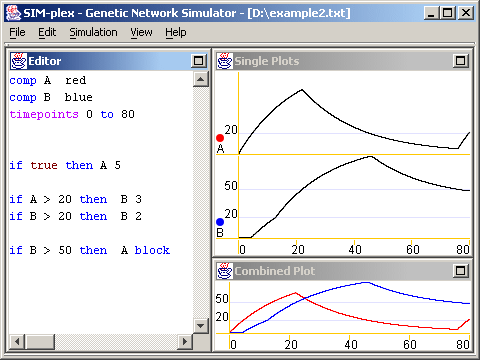
The simulator program shows three internal windows. In the image below, you see an example of its appearance after a very simple simulation.

You type the definition of a genetic regulatory network in the left window. After you choose Simulate from the Simulation menu, or simply hit F5, the right windows will show two different views of simulation results. The top window shows each geneproduct's amount through time separately, while the bottom window shows a combined view of a requested subset of the genes.

The program can export the results to a file readable by Excel (tab-delimited), so while the right windows show results quickly, creating fancy graphs can happen outside the simulator.

A quick introduction:  (for more information, look on the Manual page)

• the comp statement tells that you will use a certain component (mRNA or protein) in your network definition. It takes an optional argument that says how much component there is initially.
  If you give a color name as an extra argument, then the component will also be shown in the combined view window, for example "comp A  100  red"
   
• the timepoints statement sets the range to simulate and plot.
   
• if ... then ...  statements are the most important. After the if keyword, you can build conditions like "A > 50  and  CDKB < 25  and  ...".
  These statements are descriptive of particular interactions in a gene regulatory network. Conditions like this mimic how proteins and protein-complexes bind on the promotor of a gene and initiate, enhance or inhibit its transcription.
  After the then keyword, you can give a component's name and the rate at which this component should be created when the given conditions are satisfied.

You might wonder why the component amount of  A  decreases in the above example. The reason is that this reflects natural break-down by proteases, nucleases etc.  The rate of this degradation can be customized when you define the component with an optional third argument.
For example, "comp A  100  0.01"  would give component  A  an initial component amount of 100 units and a degradation rate of 1% per time unit.
Note that component units and time units are arbitrary. These can be numbers of molecules, concentrations, or seconds, days etc.

There are three new things to learn from this example.  (Note that it also illustrates comp's optional color argument that we already mentioned).

First, it shows a statement with the "true" condition. Here it means "always create A at rate 5".

Second, it shows that statements work additively. At each point in time, all statements that create a component P and have a condition that is true, are summed together.
In the example, when A rises above 20, B is activated and created at a rate of 3. After that, when B rises above 20, B enhances its own transcription, by creating an extra 2 component-units per time-unit. You can clearly see that the creation rate of B increases (to 3+2=5) at timepoint 12.

Third it illustrates the "block" clause. In the example it means that all creation of A will be blocked when the condition "B > 50" is true. Of course the degradation (or break-down, see further) of component A already created, will continue until this A is completely gone.
The block can also be made partial. For example, "A  block 0.15" restricts the creation of A to 15% of what would be created without the block.

This illustrates one new statement: "if ... then transform  A to B rate ". This can be used to model the transformation of a protein A to its modified form (e.g. phosphorylated), here called B. The slope in both graphs is again caused by proteolytic or RNA degradation. In the combined view you can see that the slope nicely goes over from the red to the blue graph.
(Before simulation, a transform-statement is translated to a creation part and a consumption part:  "if ... then A rate "  and  "if ... then B -rate ".  See Manual for correct details.)
More general, "... transform  (A B) to C  rate "  could model the binding of proteins A and B to a protein complex called C.

 --- We are aware that these non-regulatory biochemical operations are quantitatively less correct in the mathematical framework that we use (i.e. linear creation/consumption and exponential degradation).  However in a genetic network that is already a quantitative approximation of reality, we believe that SIM-plex still provides a very usable functionality to quickly and interactively define the global topology of switch-like networks ---

Note: it is important to define a protein and its modified form as two different components, because they are two different biochemical entities, which can be transformed into one another.

This section is for those hungry for more.
The if-then statement can have different tails, that mean different things. Here is an overview:

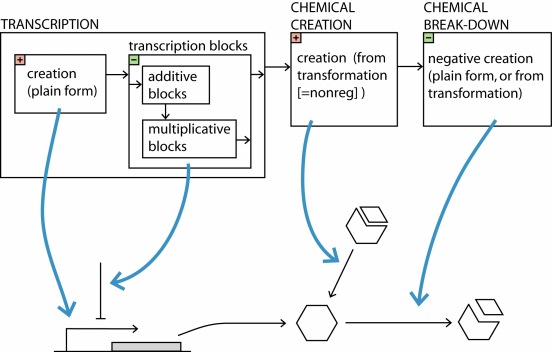
Note the difference between (2) and (4): the block-tail, and the "negative creation part".  One may NOT use additivity like adding a +5 and a -5 to stop creation under certain conditions, because this would be context-sensitive!  If the +5 would become a +8 at some time, or something else, then using "block" is the effective way to be sure that creation really stops.  "Negative creation rates" can then of course still consume still available component.

Also note the difference between (1) and (3): transcriptional creation which can be regulated by block statements, and "nonreg"-creation which can not be regulated by blocks.
For example, assume that one simulates under the rough approximation that mRNA is very quickly translated to proteins, then for all intents and purposes only one "geneproduct" is active (instead of two, mRNA and protein).  However, when some biochemical operation happens such that the protein is produced (e.g. dephosphorylation of its phosphorylated counterpart), then this biochemical production part is cannot be regulated by blocks, while the transcription part can still be under a "block" at the same time.
You will probably never use the "nonreg" tail because you will rather use the more powerful if-then-transform statement. When a transform statement is translated to two or more plain if-then-statements, these if-thens are in fact written with a "nonreg" in their tail.
Note that "A nonreg -5" would have the same effect as "A -5" because break-down always has a non-transcriptional cause, and can thus not be regulated by "block" statements.

A schematic overview:

You are now ready to start simulating,
or to dig deeper and read the Manual.